Have you noticed lately that several different cellular phone companies are running ads claiming to be America’s leading network? Have you wondered how they can all claim to be number one? One company claims to have the fewest dropped calls of any network. This sounds impressive until you begin to wonder how many calls actually connect in the first place. Companies can’t drop calls if they don’t complete them in the first place.
To understand and evaluate the wealth of information that advertising and press releases provide us, it is important to be an informed consumer. Knowing what questions to ask when reading claims in the media is crucial to becoming an active processor, rather than a passive absorber, of this information. To know what questions to ask, a basic understanding of statistics and research methodology is necessary. We attempt to provide some of that understanding in the BASIS every week. Although the research we review is important, the ability to understand and evaluate the research you come across in other settings is just as important.
I recently read a press release touting a technology able to identify players at risk for gambling problems “with a precision of more than 90%.” A very impressive claim at first glance. But let’s investigate this claim more thoroughly. What does 90% precision mean in this case? The study behind this claim is not publicly available – no surprise – so we have to speculate. Given what we know about gambling disorders and problems, it is interesting to explore what data could lead to such a claim.
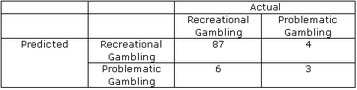
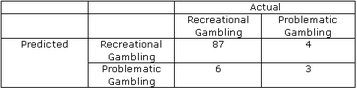
Here is one way to achieve 90% precision:
In this example, there are 7 actual gamblers with problems, and 93 actual recreational gamblers without problems, represented by the columns. The rows represent how the given model (e.g., technology, diagnostic test, etc.) classifies those people. In this case, the predictive model correctly classifies 90% of the sample (i.e., the 87 who are both predicted and are actual recreational gamblers and the 3 who are both predicted and are actual gamblers with problems). This represents the 90% precision claim. However, disordered gambling is a “low” base rate event: less than 2% of the population typically qualifies as pathological gamblers and approximately 3-5% more as problem gamblers. As a result, most people classified by any model will fall into the recreational category, both in terms of their actual and predicted symptoms.
In the example, 93 do not have gambling problems, and the model correctly classifies 94% of those 93. (1) This relationship accounts for the bulk of the model’s classification accuracy. If instead, we consider the model’s capacity to accurately classify actual gamblers with problems, a different picture emerges. There are 7 actual gamblers with problems in the example. The model correctly classifies 3 of them: 43%. (2) Of the 9 people that the model classifies as gamblers with problems, only 33% are actual gamblers with problems. (3)
There are two key points here: First, statistics can sound impressive, but without the appropriate context, statistics easily can be misinterpreted. Second, specific to a disorder or problem with a low occurrence in the general population, it is relatively easy to achieve very good overall classification accuracy. To truly evaluate a model’s ability to classify, as in this case, it is important to know how well it classifies actual cases (e.g., gamblers with problems), not just non-cases.
Protecting the public health is best served by developing screening procedures that have a high sensitivity (i.e., ability to identify those people who have problems). Assuming that the procedures themselves don’t have any extraordinary risks, it is generally optimal to include false positives (i.e., people identified as having problems who do not actually have problems) rather than to miss identifying the cases with problems. Informed consumers should demand to know all the parameters of a model’s accuracy, and in the case of infrequently occurring problems, particularly the sensitivity.
What do you think? Comments should be addressed to Sarah Nelson.
Notes
1 This (i.e., correctly classifying 94% of those without problems) is the specificity of the predictive model.
2 This (i.e., correctly classifying 43% of those with problems) is the sensitivity of the predictive model.
3 This (i.e., 3 of the 9 classified as having problem actually having problems) is the positive predictive value of the predictive model.