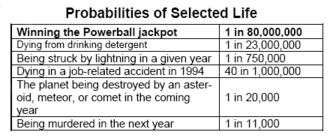
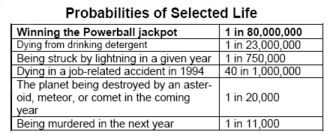
The Powerball drawing in West Des Moines last Wednesday marked a new beginning for 13 winning Ohio machinists and a long-awaited end to the troubles of Greenwich, Connecticut [1]. Powerball tickets are sold in 20 states and in the District of Columbia. Connecticut, geographically convenient to the non-Powerball, densely populated states of New York and New Jersey, has long served as a point of purchase for local and regional lottery players. Greenwich, accessible by I-95 just across the New York border, has often shouldered much of the Powerball traffic. But when the jackpot climbed toward a quarter of a billion dollars late last month, even Greenwich was unprepared. Stories abound of people dodging highway traffic, enduring gridlock, and improvising on account of the lack of public rest rooms. The state’s Attorney General suggested legislation that would allow cities to regulate Powerball sales [2] and the Governor promised $85,000 in aid to cover the overtime expenses incurred-a decision that has become a heated political debate [3]. The mechanics of Powerball are reasonably straightforward. Five white balls and one red “powerball” are drawn, yielding the odds of 80 million
to one for having the winning numbers. How can such steep odds be reconciled with the anecdotes and high sales in Greenwich and other Powerball venues?
Bernoulli’s concept of utility posits that the subjective value of money decreases as the total amount increases. By this reasoning, the perceived value of $2,000 is not twice that of $1,000, but somewhat less. Bernoulli’s notion of marginally decreasing utility is essentially a form of the law of diminishing returns. If such a utility model were to hold true in the Powerball case, then it would seem to follow that an objective measure of lottery participation (quantity of tickets sold, net revenue, media coverage, etc.) would increase proportionately as the Powerball jackpot builds. But choosing such an objective measure is problematic. External socioeconomic factors can bias gross sales and net revenue, and a relative indicator of “lottery fever” would be difficult to construct. Bernoulli’s utility functions are psychophysical; they ignore motivation and do not deal with the psychological factors of perceived risk and risk aversion. Psychologist Lola Lopes proposes a dual model for understanding the motivation of risk. Peoples’ disposition toward risky behavior is determined by their relative valuation of security and potential. A risk-seeker will find the potential payoff of a risk to be more salient than the possible threat to personal security, whereas a person who is risk-averse will forego the payoff in favor of security. Lopes’s second factor is aspiration, which refers to the situational benefits and constraints that mitigate the decision of when to engage in a risk behavior. It is the latter that seems to be at work in Powerball. That is, an incomprehensibly high jackpot may have swayed the judgment of those who are normally risk-averse while simultaneously intensifying the potential-seeking attitudes of risk-seekers [5]. Or perhaps an entirely different psychology is at work. Social psychologist John Bassili of the University of Toronto proposes that abstract probabilities and statistics are little match for concrete images of winning and consumption. Winning, then, is psychologically more salient. He also cites a phenomenon of inflation, “In the person’s mind, the ticket they selected has more value than any other ticket even though the odds are just the same” [6]. This belief system might even lead many Powerball losers to feel depressed about not having held this past week’s winning ticket.
Sources:
- Bowled over by Powerball. (1998, August 2). The New York TImes, 4:2.
- Official proposes limits to Powerball sales times. (1998, August 2). The New York Times, 1:38.
- Greenwich: Critics blast town’s powerball ‘crisis.’ (1998, July 31). The Hartford Courant, A1.
- (all probabilities except Powerball odds) A fistful of risks. (1996, May). Discover, 82.
- Lopes, Lola L. (1987). Between hope and fear: The psychology of risk. Advances in Experimental Social Psychology 20, 255-295.
- Big dreams, not odds, drive lottery players. (1998, July 31). The Toronto Star.
This public education project is funded, in part, by The Andrews Foundation and the National Center for Responsible Gaming.