Probability theory is the basis for both the academic study of statistics and the practice of gambling. Mathematicians and gamblers alike have devoted entire lifetimes to improving their understanding of probability. Probability is so deeply ingrained in our daily lives that we fail to notice its presence at all. A 30% chance of rain… 10 to 1 odds for the Red Sox winning tonight’s game… A once-in-a-lifetime opportunity… All involve the fundamental rules of probability. But just what are these rules? How to define probability is a matter of debate among mathematicians. The most common, however, states that
If an experiment is repeated n times under identical conditions, and event A occurs m times, then as n increases, the ratio of m to n is the probability that event A will occur. [1]
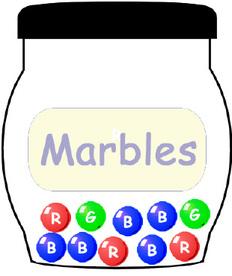
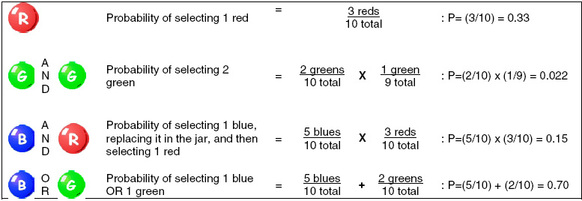
For example, if we roll a die 1,000,000 times we can expect that the probability of rolling a three is equal to the number of times we actually roll a three divided by 1,000,000. Probability is usually denoted by the letter ‘P’ and is often expressed as a decimal. Thus, the probability of rolling a six on a die is one out of six, or P =0.167. The table below illustrates some basic rules of probability using a jar of 10 colored marbles.
The idea of probability is difficult to grasp and often leads to many mistaken beliefs. For example, suppose you flip a coin 99 times and each time the coin lands on ‘heads.’ Many people believe that you have an excellent chance of getting a ‘tails’ on the 100th flip. This is not true. The probability of getting a ‘tails’ on the 100th flip is the same as it is for the 1st, 2nd, and 98th flip. Mistaken ideas about probability are common among pathological gamblers. These false beliefs may be corrected with the use of cognitive therapy [see WAGER 4(47) and WAGER 4(7)].
References
[1] Pagano, M., & Gauvreau, K. (1993). Principles of biostatistics. Belmont, CA: Duxbury Press. p.116.